 |
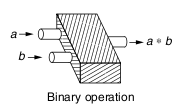
Sebenernya saya sudah pernah membuat tulisan mengenai operasi biner tapi kali ini saya ingi membahas operasi biner secara lebih mendalam. Kalau saya analogikan operasi biner adalah sebuah “mesin” yang memepunyai dua buah input dari elemen2 di suatu himpunan tak kosong S dengan output satu elemen di S juga. Jika “mesin” tersebut hanya mempunyai satu input dan satu ouput maka dikatakan operasi unary
Diberikan S adalah suatu himpunan tak kosong, himpunan S×S adalah himpunan yang memuat semua pasangan (a,b) dengan 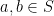 . Suatu operasi biner
. Suatu operasi biner  pada S sebenarnya merupakan fungsi dari S×S ke S. Dinotasikan image (daerah hasil) pasangan (a,b) dengan
pada S sebenarnya merupakan fungsi dari S×S ke S. Dinotasikan image (daerah hasil) pasangan (a,b) dengan 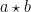 . Dengan kata lain operasi biner
. Dengan kata lain operasi biner  memetakan dua buah elemen a dan b di S ke suatu elemen
memetakan dua buah elemen a dan b di S ke suatu elemen 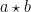 di S pula.Opersi biner sering dikatakan tertutup untuk menegaskan bahwa
di S pula.Opersi biner sering dikatakan tertutup untuk menegaskan bahwa 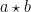 termuat di S, bukan di himpunan di luar S. Banyak simbol yang digunakan untuk operasi biner, yang umum digunakan adalah
termuat di S, bukan di himpunan di luar S. Banyak simbol yang digunakan untuk operasi biner, yang umum digunakan adalah 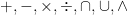 dan
dan 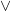 .
.
Diberikan 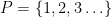 himpunan bulat positif. Penjumlahan dan perkalian merupakan operasi biner di
himpunan bulat positif. Penjumlahan dan perkalian merupakan operasi biner di 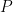 karena untuk sebarang
karena untuk sebarang 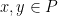 berlaku
berlaku 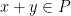 dan
dan 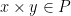 . Tetapi pengurangan bukan operasi biner di
. Tetapi pengurangan bukan operasi biner di 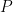 karena
karena 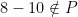 . Contoh operasi biner yang lain di
. Contoh operasi biner yang lain di 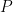 adalah perpangkatan dan FPB.
adalah perpangkatan dan FPB.
Penjumlahan, perkalian, pengurangan kesemuanya merupakan operasi biner di himpunan bilangan real 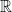 karena a+b, a×b, x-y merupakan bilangan real untuk setiap pasang a dan b bilangan real. Pembagian bukan merupakan operasi biner di
karena a+b, a×b, x-y merupakan bilangan real untuk setiap pasang a dan b bilangan real. Pembagian bukan merupakan operasi biner di 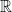 karena pembagian dengan nol tidak terdefinisi. Tetapi pembagian merupakan operasi biner di
karena pembagian dengan nol tidak terdefinisi. Tetapi pembagian merupakan operasi biner di 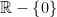 himpunan bilangan real tak nol.
himpunan bilangan real tak nol.
Operasi Biner pada himpunan berhingga umunya disajikan melalui tabel. Sebagai contoh diberikan himpunan 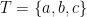 yang memuat 3 elemen. Operasi biner
yang memuat 3 elemen. Operasi biner  pada T didefiniskan berdasarkan tabel 1.1 berikut
pada T didefiniskan berdasarkan tabel 1.1 berikut

Tabel tersebut dibaca baris dioperasikan kolom, contoh 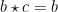 ,
, 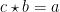 . Nah sekarang pertanyannya bagaimana mendefinisikan tabel di atas? Itu sich terserah yang buat tabel
. Nah sekarang pertanyannya bagaimana mendefinisikan tabel di atas? Itu sich terserah yang buat tabel 
Suatu operasi biner  pada himpunan S dikatakan
pada himpunan S dikatakan
- asositif jika berlaku
untuk semua
- Komutatif jika berlaku
untuk semua
Suatu elemen 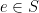 dikatakan identitas jika berlaku
dikatakan identitas jika berlaku 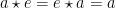 untuk semua
untuk semua 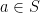 .
.
Diberikan operasi biner  pada himpunan S yang mempunyai identitas
pada himpunan S yang mempunyai identitas  , elemen
, elemen 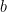 dikatakan invers dari
dikatakan invers dari  jika berlaku
jika berlaku 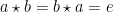 dengan
dengan 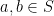 . Pada umunya invers
. Pada umunya invers  dinotasikan
dinotasikan
Diberikan2 operasi biner  dan
dan  pada himpunan S. Operasi
pada himpunan S. Operasi  dikatakan distributif atas
dikatakan distributif atas  jika berlaku
jika berlaku 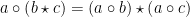 dan
dan 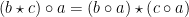 untuk semua
untuk semua 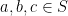
Penjumlahan dan perkalian keduanya merupakan operasi asosiatif dan komutatif pada himpunan bilangan real 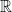 . Identitas penjumlahan adalah 0 dan identitas perkalian adalah 1. Setiap bilangan real mempunyai invers atas penjumlahan sedangkan setiap bilangan real tak nol mempunyai invers atas perkalian. Selain itu perkalian bersifat distributif atas penjumlahan karena berlaku
. Identitas penjumlahan adalah 0 dan identitas perkalian adalah 1. Setiap bilangan real mempunyai invers atas penjumlahan sedangkan setiap bilangan real tak nol mempunyai invers atas perkalian. Selain itu perkalian bersifat distributif atas penjumlahan karena berlaku 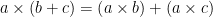 dan
dan 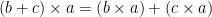 . Tetapi penjumlahan tidaklah bersifat distributif atas perkalian karena
. Tetapi penjumlahan tidaklah bersifat distributif atas perkalian karena 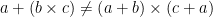 tidak berlaku secara umum.
tidak berlaku secara umum.




0 komentar:
Posting Komentar